運算思維(Computational Thinking)在近年來逐漸被關注資訊教育的人們提出來討論。而運算思維包含了問題解構(Decomposition)、型樣辨識(Pattern Recognition)、模型抽象化(Abstraction)以及演算法設計(Algorithm Design)。
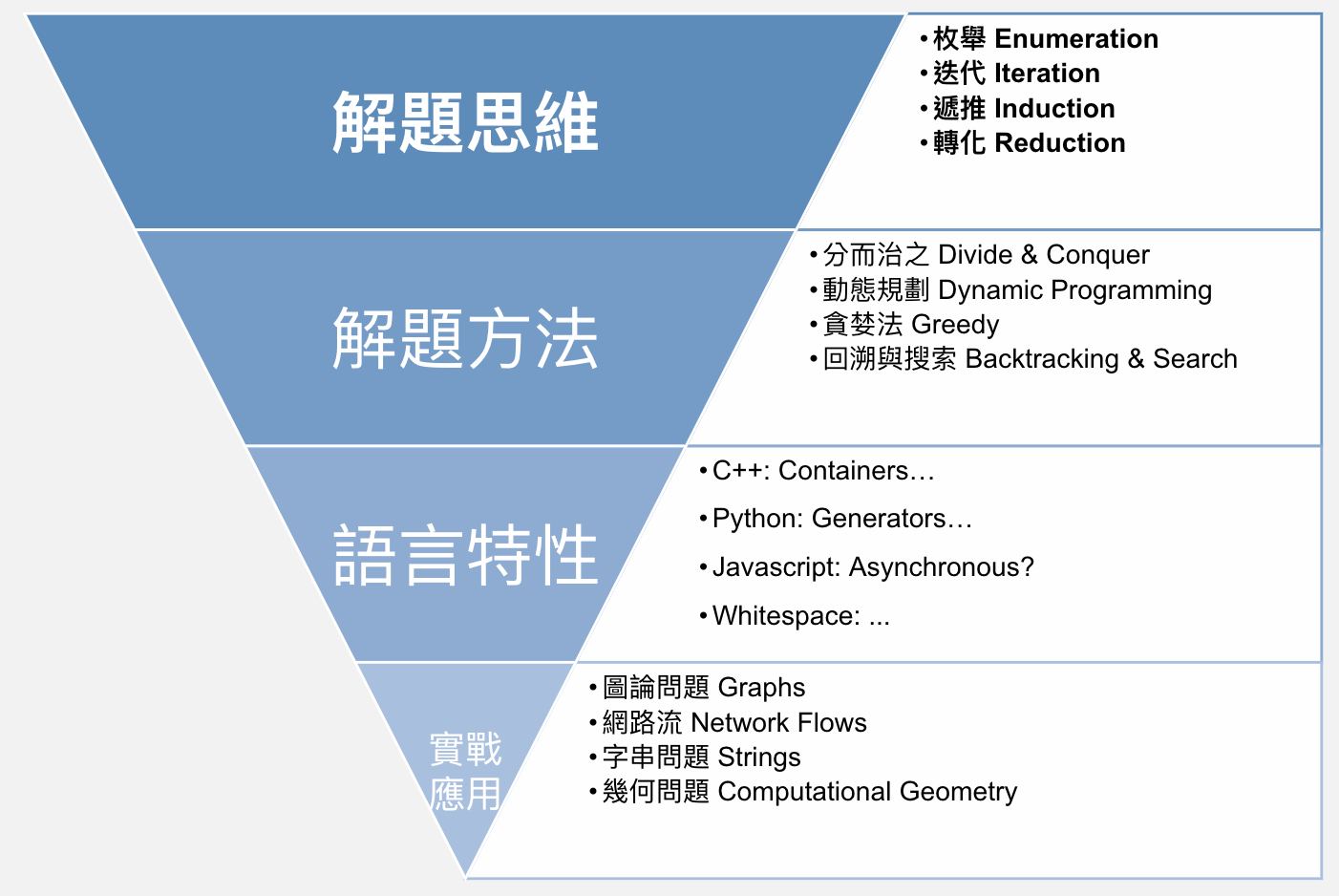
對我來說,演算法設計的世界裡面,解題的過程也可以大致分類成以下四種思考方式。而這些思考方式構建了大家在演算法教科書中提及的各種解題方法(又稱為 Algorithmic Paradigm),比方說動態規劃或是分而治之等。大致可以表示成以下的圖片:
枚舉 Enumeration
程式解題與數學解題其中一個不同之處,在於我們擁有運算資源,可以把複雜的、難以公式化的數學結論,用跑程式的方式輕鬆驗證。枚舉(Enumeration)就是其中一種很「資訊科學」的解題方式:如果我能夠證明我的答案在某個特定的範圍中,那麼我只要逐一考慮過所有可能的答案即可。
簡而言之,若一道題目滿足以�下兩個性質:
- 若給定一個解 X,我們可以有效率地檢驗 X 是否正確。
- 把可能的解所在的範圍,縮小到足以負擔的數量級。
那麼通常我們可以寫出好寫又有效率的程式。
迭代 Iteration
迭代法,通常是用於我們可以逐漸找出答案的演算法。最常見的應用是漸進演算法、數值方法、人工智慧等。在競賽之中,我們也可以利用迭代的概念,有效率地得出我們想要的解。最直白的應用就是 for 迴圈。對,還有 while 迴圈。
遞推 Induction
在驗證程式邏輯的正確性的時候,我們很常會使用數學歸納法:「如果小測資是對的,那麼根據我們解題的思路,也可以推得大測資是對的。」P老師也曾經說過:「歸納」、「遞迴」跟「分而治之」其實是一體三面,對於有效率地寫程式解決問題是相當重要的。
轉化 Reduction
轉化跟歸納其實是兩個不同的方向:如果說歸納是以建構的方式,由小範圍的測資組合出大範圍測資的答案,那麼轉化有點像是平行地把一個問題轉變成另一個已知解法問題。轉化在解題思維中無所不在,畢竟大家在面對一道新的題目時,總是會習慣搜尋自己曾經解決過的類似題目、並且利用以前的經驗,把思路稍作修改從而獲得真正的解法。