Borůvka 樹分治（一）：直線上的 Borůvka

今天我們聊聊比較輕鬆的話題。 在邁向更多的最小生成樹演算法之前，我們先來看幾個例子：在一些相對單純的圖上面跑 Borůvka 演算法。我們發現在一條簡單路徑、或是在一棵樹上直接執行 Borůvka 演算法，會得到一個有趣的、充滿單調性的資料結構。而這個結構（我們不妨稱之為 Borůvka 樹分治），可以幫助我們解決一類常見的靜態離線區間極值問題。

前情提要

Borůvka 演算法是由不超過 \(O(\log n)\) 個 Borůvka 步驟組成。在每一個 Borůvka 步驟中，我們對所有的點挑選往最小權重的外連邊，這些邊（可能會被重複挑選）將形成一個森林。將該森林的所有連通元件全部縮起來變成一個點，並且移除所有的自連邊、並在所有重邊中留下權重最小的一條，結束這個 Borůvka 步驟。

Borůvka 演算法跑在什麼樣子的圖是有效率的呢？下面這個引理率先給了三個例子。

引理 MST.12

1. 如果輸入的圖是一條簡單路徑，那麼在上面跑 Borůvka 演算法只需要 \(O(n)\) 的時間。
2. 如果輸入的圖是一棵樹，那麼在上面跑 Borůvka 演算法只需要 \(O(n)\) 的時間。
3. 如果輸入的圖是簡單平面圖，那麼在上面跑 Borůvka 演算法只需要 \(O(n)\) 的時間。

引理 MST.12 的概略證明

首先，不難發現一條簡單路徑、樹、簡單平面圖，其邊數都是 \(O(n)\) 的。 經過一次 Borůvka 步驟以後，縮起來的圖也分別仍是一條簡單路徑、樹、簡單平面圖。但根據引理 MST.7，每縮一次點數至多剩一半。因此整體的時間複雜度是 \(O(n + n/2 + n/4+\ldots) = O(n)\)。

接下來，我們來探索一下 Borůvka 步驟帶給我們的有趣性質吧！

在直線上進行 Borůvka 步驟

如果這張圖是一條簡單路徑，那麼進行一次 Borůvka 步驟以後， 形成的森林也都會是由簡單路徑組成，如下圖所示：

這些森林並不是任意的簡單路徑！如果我們多看兩眼，而且把「每條邊被哪一個點選中」的理由用一個箭頭表示，那麼我們會發現，每一個連通的簡單路徑，其邊的權重都是先遞減再遞增的。

若重複進行 Borůvka 步驟，那麼把這些步驟依序畫出來，可以用一棵樹狀結構來表示。這棵樹的深度取決於進行 Borůvka 步驟的次數，而且最大深度不超過 \(\log n\)。

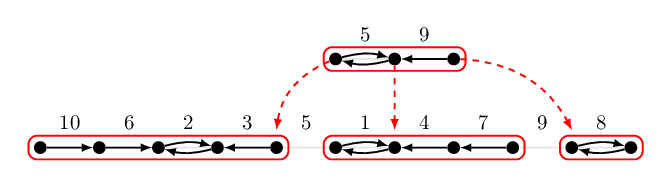
這個先遞減再遞增的特性，可以幫助我們回答下面這個問題：

區間最大值問題

給定一個序列 \(a_1, a_2, \ldots, a_n\) 以及 \(m\) 筆詢問 \(\{[l_i, r_i]\}_{i=1}^m\)。對於每一個詢問 \(i\) 我們想知道區間內的最大值 \(\max_{l_i\le j\le r_i} a_j\)。

如上面圖片給的例子，我們的輸入是 \(n=10\)、\(a=[10, 6, 2, 3, 5, 1, 4, 7, 9, 8]\)。如果我們想知道詢問 \(L=2, R=4\) 的答案，也就是 \([6, 2, 3]\) 之間的最大值，我們可以先看看在最底層 \(L\) 和 \(R\) 是否屬於第一次 Borůvka 步驟的連通元件。如果是的話，根據先遞減再遞增的特性，此時必定有 \(\max_{L \le j\le R} a_j = \max(a_L, a_R)\)。換句話說，這時候我們只需要檢查兩個數字就可以得知答案了！

如果是另一個情形：詢問的兩個邊界並不屬於第一次 Borůvka 步驟的連通元件。那麼我們可以依循剛才建構出的樹狀結構，同時讓兩個邊界往上爬，直到它們出現在同一個連通元件為止。在往上爬的過程中，記錄下經過的所有連通元件中的相鄰邊，裡面出現的最大值就是我們要的解。

由於樹的高度只有 \(O(\log n)\) 甚至更小，因此每一次詢問需要的時間是 \(O(\log n)\)。

係理 MST.13

存在一個 \(O(n)\) 時間預處理、\(O(\log n)\) 時間回答每個區間最大值詢問的演算法。

為什麼標題叫做樹分治？

在下一篇文章中，我們將重新看待這個樹狀結構。King 在 1997 年發表的論文¹中，將上述的想法給出更具體的轉化 (Reduction)，而且她的方法也適用於輸入不僅僅是一個序列，還可以是一棵樹。

備註

對於區間極值問題，是存在 \(O(n)\) 時間預處理、\(O(1)\) 時間回答區間最大值的演算法的。不過該演算法需要使用查表技術，這個技術通常被稱為間接查表 Indirection² 或是四俄羅斯人方法 Methods of Four Russians³。