最少比較排序

前一篇我們討論了比較排序的下界。對於所有的 \(n\)，基於比較的排序方法至少要花 \(\ceil{\log n!}\) 次比較。而根據合併排序法、或快速排序法等，我們也知道要完成排序至多只需要 \(O(n\log n)\) 次比較。 Lower bound 與 Upper bound 完美地合起來了不是嗎！俗話說得好，魔鬼藏在細節裡，常數藏在 big-O 裡面。對於六〇年代的電腦科學家們，不把常數寫清楚是會對自己過意不去的。換句話說，若先不考慮把演算法實作出來後真正的時間複雜度，我們只關心「比較次數」的話，是否總是存在一種排序的演算法，在最壞情形下只需要恰好 \(\ceil{\log n!}\) 次比較就能夠排好序呢？

答案是否定的。但是在描述最小反例之前，我們不妨先想想看，究竟可以設計出怎麼樣的演算法，其所需的比較次數與 \(\ceil{\log n!}\) 足夠接近：

引理 20

存在一種比較排序法，使得排好 \(n\) 筆資料至多需要 \(\ceil{\log 2} + \ceil{\log 3} + \cdots + \ceil{\log n}\) 次比較。

引理 20 的證明

上面這個式子給我們很大的提示：我們只要稍微修改一下插入排序法，每一次加入一個數字。但是在加入的時候，我們不從當前序列末端一路比較過來；相反地，我們使用定理 19 提到的二分搜尋法，把資料插入目前排好序的序列就可以了。我們不需要擔心資料搬移所花費的時間，反正資料的搬移在這個比較次數至上的計算模型裡面是免費的！

看來細節不只藏在 big-O 裡面，還藏在天花板裡面呢。

上面這兩個函數到底差多少？令 \(A(n) = \ceil{\log n!}\)、令 \(B(n) = \sum_{i=1}^n \ceil{\log i}\)。我們可以簡單寫張表，列出前面幾項數值：

\(n\)	1	2	3	4	5	6	7	8	9	10	11	12
\(A(n)\)	0	1	3	5	7	10	13	16	19	22	26	29
\(B(n)\)	0	1	3	5	8	11	14	17	21	25	29	33

在 \(n=5\) 的時候數字就不一樣了！這不禁讓我們思考：要排好 5 個數字，至少需要進行幾次比較呢？如果是 7 次，那麼代表前述之「二分插入法」不能達到最少比較次數；反之，如果是 8 次，代表基於資訊理論方法得到的下界不是最緊的。無論是哪一種結論好像都讓我們多理解了什麼，對吧～

引理 21

存在一個比較排序法，使得正確排序 5 筆資料，在最壞情形下僅需要 7 次比較。這結果真的是令人五筆振奮啊（這裡沒有梗）。

引理 21 的證明

證明實在難以用言語形容，直接畫圖比較快。這邊我們假設輸入為 \(A[1..5]\)。

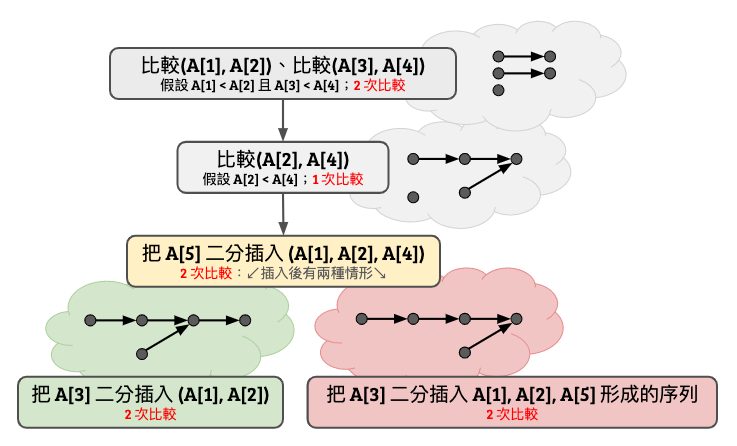
你看看，無論輸入長什麼樣子，這個決策樹總可以在至多 7 次以內順利排序完畢。而這邊使用到的是二分插入法的概念，只是用了比較取巧的比較順序。西元 1959 年 Ford-Johnson 把這個想法延伸，設計出了一個叫做合併插入排序法 Merge Insertion Sort 的排序演算法（其中 Ford 就是 Ford-Fulkerson 演算法裡面的 Ford、Johnson 就是 Johnson 演算法裡面的那位、好吧我不知道我在講什麼。）

如果我們把 FJ 演算法需要的比較次數的前幾項寫出來：

\(n\)	1	2	3	4	5	6	7	8	9	10	11	12
\(A(n)\)	0	1	3	5	7	10	13	16	19	22	26	29
\(FJ(n)\)	0	1	3	5	7	10	13	16	19	22	26	30

從 \(n=2...11\) 全部都是最佳解了！真正難纏的部分是 \(n=12\)，直到 1965 年 Mark Wells¹ 率先撰寫程式列舉所有排序結構，證明了 \(S(12) = 30\)（有興趣的朋友可以參考 Knuth 的 TAOCP，第三卷）。這個結果證明了資訊理論下界不等於最少排序次數。

Ford-Johnson 的合併插入排序法是否真的是最優的呢？可惜的是 1977 年 Manacher² 否定了這件事情：他證明了存在無窮多個 \(n\)，使得最少排序次數比 \(FJ(n)\) 嚴格來得小。目前已知最小的反例是在 \(n=189\)。

如同四色定理一樣，找出最少比較排序的次數，可以藉由電腦輔助而完成證明。很酷吧！

演算法的分析與證明

最少比較排序

引理 20

引理 20 的證明

引理 21

引理 21 的證明

推薦閱讀