偏序集排序（四）

為了繞過使用深奧隨機走訪方法與馬可夫鏈而得到的估計 \(e(P)\) 近似演算法， 我們今天把這個順序多胞形轉換一下，變成另一個直鏈和多胞形（Chain Polytope）。

直鏈和多胞形 Chain Polytope

在 poset \((P, <)\) 上面的一條直鏈（chain） \(C\subset P\)，其實就是一個任兩元素都可以比較的子集合。 我們考慮以下的直鏈和多胞形（chain polytope）：

\[ \mathcal{C}(P) = \{ (z_1, \ldots, z_n) \ \vert \ \forall \text{ chain } C, 0\le \sum_{x_i\in C} z_i \le 1 \} \]

換句話說，只要 \(n\) 個介於 \([0, 1]\) 之間的實數，滿足對於 poset 之中任何一條直鏈，它對應數字的總和不超過 \(1\) 的話，這個點就會被我們加入多胞形之中。

兩個多胞形之間的轉換

要怎麼找出直鏈和多胞形 \(\mathcal{C}(P)\) 與順序多胞形 \(\mathcal{O}(P)\) 之間的關聯呢？ 試想像一下，如果我們有一條鏈：

那麼 \((0.1, 0.3, 0.05, 0.2, 0.05, 0.3, \ldots)\in \mathcal{C}(P)\)。由於在 \(\mathcal{C}(P)\) 上頭，每一條鏈上面的數值總和都不超過 \(1\)，透過 前綴和（Prefix Sum） 的概念，我們可以定義出一條非遞減的序列如下：

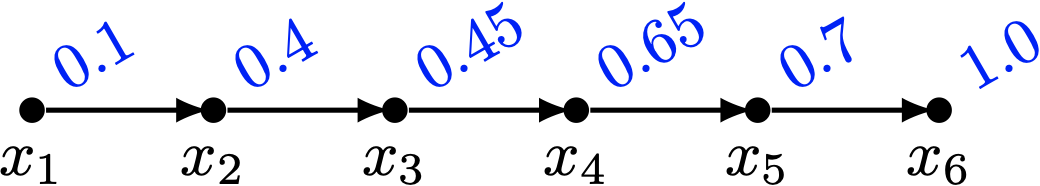
每一個點的數值變成了這條鏈上面它所有祖先原本的數值總和，加上自己本身的數值。 不難發現，現在這個賦值方式滿足順序多胞形的條件： \[ (0.1, 0.4, 0.45, 0.65, 0.7, 1.0, \ldots) \in \mathcal{O}(P) \]

現在讓我們來考慮推廣版的情形：如果一個點屬於超過一條鏈怎麼辦呢？對於一個點 \(z=(z_1, \ldots, z_n)\in\mathcal{C}(P)\)，我們可以定義出一個點 \(\varphi(z) = (z'_1, \ldots, z'_n)\in\mathcal{O}(P)\)，其中 \(z'_i = z_i + \max_{j: x_j < x_i} z'_j\)。這個轉換 \(\varphi\) 其實也是一一對應的：對於一個點 \(z' = (z'_1, \ldots, z'_n)\in\mathcal{O}(P)\)，我們可以回推出 \(\varphi^{-1}(z') = (z_1, \ldots, z_n)\in\mathcal{C}(P)\)，使得 \(z_i = z'_{i} - \max_{j: x_j < x_i} z'_j\)。

因此我們可以說：對於任意偏序集，都存在一個雙射變換 \(\varphi_P: \mathcal{C}(P)\to \mathcal{O}(P)\)。可惜的是，光憑這個結論，我們無法斷定這兩個多胞形的體積關係。這時候，就是我們前一篇介紹的 Ehrhart 多項式派上用場的時候啦！

定理 25 [Stanley 1986]1

對於任何偏序集。\(\mathcal{C}(P)\) 的體積與 \(\mathcal{O}(P)\) 的體積相等。

證明

還記得我們說過多胞形的 Ehrhart 多項式嗎？如果把 \(\mathbb{R}^n\) 空間中，每一個座標軸放大整數倍 \(k\)，那麼多胞形內部的格子點（所有座標都是整數的點）的數量會以 \(\Theta(k^n)\) 的速度成長，而這個點數可以被一個 \(n\) 次多項式表示之。

換句話說，如果我們有辦法證明 \(\mathcal{C}(P)\) 與 \(\mathcal{O}(P)\)，在座標軸放大任意整數倍之後，格子點數仍然相同，那麼很顯然它們有一模一樣的 Ehrhart 多項式（任何一個 \(n\) 次單變數多項式可以被 \(n+1\) 個取值唯一決定。）

而這個整數點格子數量的結論顯然是正確的：在放大 \(k\) 倍之後，若 \(kz = (kz_1, kz_2, \ldots, kz_n)\) 是格子點，那麼根據 \(\varphi\) 的定義，在變換之後 \(\varphi(kz) = kz'\) 也會是格子點。反之亦然。於是，我們就得證啦～

這個直鏈和多胞形有什麼好處呢？它其實有另一個等價的定義：如果我們從偏序集 \(P\) 當中，任何兩個可以比較的元素對，都建立一條邊，我們會得到一個無向圖 \(G(P)\)。\(G(P)\) 也被稱為 \(P\) 的可比較圖（Comparability Graph）。

而 \(\mathcal{C}(P)\) 呢，它會恰好等於所有 \(G(P)\) 上面所有「獨立集（stable set, independent set）」所對應到的單位向量，與原點形成的凸組合（convex combination）空間。

明天我們來看看這個 \(G(P)\) 的補圖 \(\overline{G(P)}\) 不可比圖（incomparability graph），他對於 \(e(P)\) 的估計有什麼厲害的幫助吧！