偏序集排序（一）

在比較排序的過程中，我們不斷地詢問某兩筆資料之間的大小關係。 到目前為止，我們知道，從資訊理論的角度來看，若採用兩兩資料比較的方式逐漸取得訊息， 從一個「完全不知道訊息之間大小關係」，與「知曉任兩筆資料之間的大小關係」， 至少要經過 \(\ceil{\log n!}\) 次詢問。

如果我們想要證明更嚴謹的排序次數下界（比方說最小反例 \(S(12) > 29\)）。我們必須要考慮所有的排序方法：證明任何一種排序方法都無法在 29 次比較之內得到 12 筆資料的完整排序。 但是，演算法顯然有無窮多種（想像一下：若我們將演算法以 C 語言實作，雖然都是排序 12 筆資料，但是有無窮多種寫法可以正確地排序這 12 種資料。） 在只關心比較次數的情況下，我們是否有辦法系統性地描述「訊息逐漸揭露」的過程呢？

要理解這個問題，讓我們從定義偏序集（Partially Ordered Sets） 開始吧！

偏序集 Poset

首先，我們不妨假設任何兩筆輸入的資料都不相同，而且所有資料存在一個全序排列（Total Order），也就是說，隨意選取任何兩筆資料 \(x\) 和 \(y\)，必定有 \(x < y\) 或者 \(x > y\)。

假設某個演算法今天對於 \(n\) 筆資料，抓了其中兩筆資料 \(x_1, x_2\) 來比較大小，獲得了 \(x_1 < x_2\) 這樣的資訊。於是呢，我們可以從 \(x_1\) 到 \(x_2\) 畫一個箭頭 \(x_1\to x_2\)。這些資料與資料之間的關聯，形成一個偏序集 Partially Ordered Set，通常我們會簡稱 Poset，以 \((P, <)\) 表示。 這個偏序集，就相當於我們目前「已知」的所有資訊。一個超級粗略的估計如下：\(n\) 個元素的 Poset 至多有 \(2^{n^2-n}\) 種¹，因為這個集合當中、任何兩個元素之間的關係要嘛可以出現、要嘛不能出現。 由於我們今天舉的例子是 \(n=12\)，讓我先把 \(n=12\) 筆資料的 Poset 數量列出來提供參考：\(414864951055853499\)。總之是個有限的數字！

要如何找出排序 \(n=12\) 筆資料的最小排序方法數呢？我們可以利用 動態規劃 的概念來解它！ 對於任何一個偏序集 \(P\)，定義 \(dp(P)\) 表示完成排序尚需要的最少比較次數。 不難發現，一開始我們掌握的資訊量是一個空的偏序集 \(P_\emptyset\)，所求的最少比較次數 \(S(12) = dp(P_\emptyset)\)。

假設我們現在手上有個偏序集 \(P_0\)，第一步該做什麼呢？我們可以選擇任何兩筆資料 \(x_i, x_j\) 進行比較。無論獲得什麼結果，我們會得到另一個偏序集 \(P_1 = P_0(x_i \lessgtr x_j)\)。注意到，如果 \(x_i\) 與 \(x_j\) 在 \(P_0\) 之中不存在任何關聯，那麼新的偏序集的大小必定大於原本的 \(|P_1\vert > \vert P_0\vert \)。 如果我們事先計算好，對所有 \(i, j\)，到底產生出來的偏序集，其最糟情形下會需要幾次比較。選取最小的那組 \((i, j)\) 就可以了！寫成遞迴關係會變成：

\[ dp(P_0) = 1 + \min_{i, j} \left( \max\{dp(P_0(x_i < x_j)), dp(P_0(x_i > x_j))\} \right) \]

對於 \(n=12\) 筆資料而言，我們就獲得一個 \(n^2\times 414864951055853499\) 時間複雜度的動態規劃演算法了！真是好棒棒。這個數字可能有點大，如果我們只考慮同構（Isomorphic） 的偏序集，那這個數字可以降到 \(n^2\times 1104891746\)，感覺變得可以負擔了。在這邊「同構」是這樣定義的：把輸入的資料 ID 隨意亂序置換以後，產生的所有偏序集都會被視為同構。顯然這些偏序集距離完全排好順序所需要的比較次數都相同，一旦計算出其中一個偏序集的 \(dp\) 值，就等同於計算出了所有其他同構的偏序集的 \(dp\) 值。

有向無環圖 Directed Acyclic Graph

在我們要討論的主題中，偏序集與有向無環圖（Directed Acyclic Graph, DAG）其實有著非常相似的概念： 我們可以利用 DAG 來表達一個 Poset \(P\)，考慮一個圖 \(G_P\)，其頂點集合就是所有的 \(n\) 筆資料 \(x_1, x_2, \ldots, x_n\)。只要在 Poset 裡面 \(x_i < x_j\)，我們就加上一條 \(x_i\to x_j\) 的有向邊（arc）。

如果這 \(n\) 筆資料是完全排序的，那麼對應到的圖 \(G_P\) 會是一個完全圖、而且它唯一的拓撲排序 Topological Order 就是把所有資料排序後的結果。 藉由圖論，我們可以舉一個 \(n=5\) 的例子，把上面的動態規劃解釋得更美觀一點～

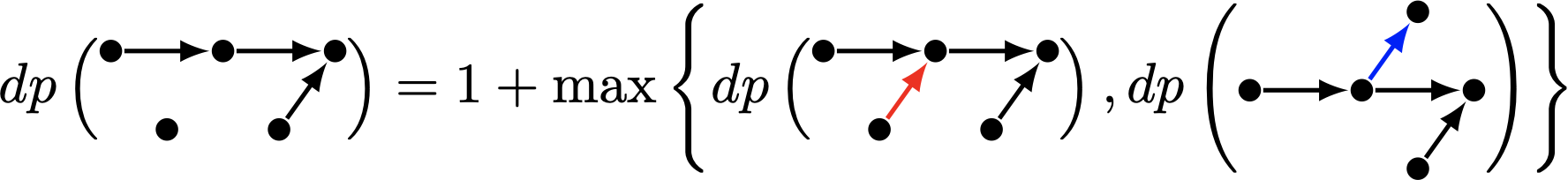
明天來繼續講偏序集與完全排序之間的更多關係！

延伸閱讀

• 張志鴻教授：數學如何定義「關係」