堆積排序法

堆積（Heap）是一種陣列資料結構。若我們將 \(n\) 筆資料的堆積以 \(A[1..n]\) 來表示的話，那麼堆積將滿足：對所有 \(x\)，\(A[x] \ge A[2x]\) 以及 \(A[x] \ge A[2x+1]\)（或是指定位置不存在資料）。我們可以按照註標將陣列資料排列成樹狀的結構：

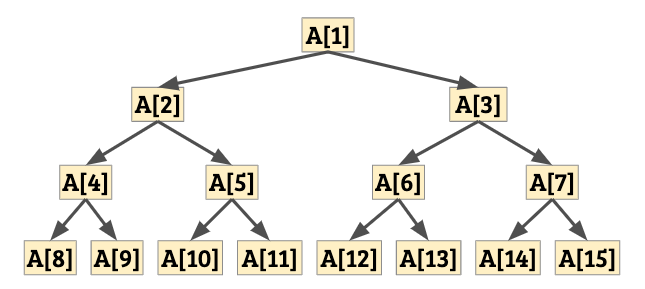
由於每一個節點內所代表的資料都比其子節點來得大，通常我們把這樣的堆積稱為最大堆積（Max-Heap）。相反地，如果我們維護的條件是 \(A[x] \le \min(A[2x], A[2x+1])\)，那麼我們會稱它為最小堆積。

定義

我們說 \(A[x]\) 滿足堆積性質，若對於所有樹狀結構中 \(A[x]\) 的子樹內節點 \(A[y]\)，都有 \(A[y] \ge \max(A[2y], A[2y+1])\)。即，如果我們把整個子樹的資料拿出來放在另一個陣列中，那它將是最大堆積。

不難發現，如果 \(A\) 是最大堆積，那麼 \(A[1]\) 的值是整個陣列中所有資料的最大值。

Heapify - 作一個整理成堆積的動作

要怎麼把一個陣列整理成堆積呢？我們只需要一種核心操作「向下交換」：

void RollDown(data_t *A, const int n, int x) {
  // 邊界條件。
  if (2*x > n) return;
  // 看成樹狀結構時，只有左子樹、沒有右子樹。
  if (2*x+1 > n) {
    if (A[x] < A[2*x]) {
      swap(A[x], A[2*x]);
    }
    return;
  }
  // 若兩邊子樹都存在，則挑大的那邊交換下去，並且遞迴處理。
  if (A[x] < max(A[2*x], A[2*x+1])) {
    int larger = (A[2*x] > A[2*x+1] ? 2*x : 2*x+1);
    swap(A[x], A[larger]);
    RollDown(A, n, larger);
  }
}

引理 16

若 \(A[2x]\) 與 \(A[2x+1]\) 分別滿足堆積性質，那麼呼叫 RollDown(x) 以後，\(A[x]\) 將滿足堆積性質。

可以利用數學歸納法來證明：假設對於所有的 \(x' > x\) 都已成立。那麼對於現在這個 \(x\) 來說，在呼叫 RollDown(x) 以後，首先我們能保證 \(A[x] \ge \max(A[2x], A[2x+1])\)。接下來，我們檢視哪些元素被動過了：如果剛才交換的是 \(A[x]\) 與 \(A[2x]\)，那麼另一邊（\(A[2x+1]\)）整棵子樹是不會變的。此時，根據歸納假設 \(2x > x\)，顯然在呼叫下一層遞迴之前，\(A[4x]\) 與 \(A[4x+1]\) 的資料都沒有變動過，因此它們滿足堆積性質。在呼叫遞迴之後，\(A[2x]\) 便滿足了堆積性質，從而得證 \(A[x]\) 也滿足堆積性質。根據對稱性，如果剛才交換的是 \(A[x]\) 與 \(A[2x+1]\)，也會保證遞迴執行完畢後，\(A[x]\) 也滿足堆積性質。

有了引理 16 以後，我們就可以輕鬆把整個陣列變成堆積了：

void Heapify(data_t *A, const int n) {
  // 注意這邊有別於一般陣列：傳入之陣列範圍是 A[1]...A[n]。
  for (int x = n; x >= 1; --x) {
    RollDown(A, n, x);
  }
}

正確性可以利用引理 16 輕鬆證得，比較有趣的是時間複雜度的分析。

引理 17

Heapify() 的時間複雜度為 \(O(n)\)。

證明

對於每一個註標 \(x\)，呼叫 RollDown(x) 時，每一次遞迴呼叫時至少將參數乘以 2，直到超過 \(n\) 為止。因此單次呼叫 RollDown(x) 的執行時間不超過 \(\ceil{\log\frac{n}{x}}\)。把它全部加起來，會得到

\[ \begin{aligned} T(n) \le \sum_{x=1}^n \ceil{\log \frac{n}{x}} &\le \sum_{x=1}^n \left(1 + \log \frac{n}{x}\right)\\ &\le n + \sum_{x=1}^n \log \frac{n}{x} \end{aligned} \]

令 \(S(n) = \sum_{x=1}^n \log\frac{n}{x}\)。推敲一陣可知 \[ S(n) = {\color{purple}{\sum_{x=1}^{n/2} \log\frac{n/2}{x}}} + {\color{green}{\frac{n}{2} + \sum_{x=n/2+1}^n \log\frac{n}{x}}} \le {\color{purple}{S(n/2)}} + {\color{green}{n}} \]

於是一路推敲下去可以用數學歸納法證得 \(S(n)\le 2n\)。所以 Heapify 整體時間複雜度為 \(T(n) \le n + S(n) \le 3n = O(n)\)。

堆積排序

有了堆積以後，就可以進行堆積排序囉。注意到，一個最大堆積其最大值總是出現在 \(A[1]\) 的位置。因此，我們可以重複地將最大值放到堆積的末端（第一次交換 \(A[1]\) 與 \(A[n]\)、第二次交換 \(A[1]\) 與 \(A[n-1]\)、依此類推）最終就可以得到一個由小到大排好順序的序列啦！

void HeapSort(data_t *A, int n) {
  // 注意這邊有別於一般陣列：傳入之陣列範圍是 A[1]...A[n]。
  Heapify(A, n);
  while (n > 1) {
    swap(A[1], A[n--]);   // 把最大值放到最後一格，並縮減堆積範圍。
    RollDown(A, n, 1);    // 整理完後又是一個最大堆積！
  }
}

這個方法的時間複雜度是 Heapify 的時間、加上執行 \(n\) 次 RollDown() 的時間。前者耗費 \(O(n)\)、後者耗費 \(\sum_{i=1}^n \log i = \Theta(n\log n)\)。因此總執行時間為 \(O(n\log n)\)。

備註

這個排序方法所需要的額外空間是 \(O(1)\)，因此堆積排序法是一種原地演算法。

演算法的分析與證明